Xin chào tất cả các bạn
fx 880 BTG có rất nhiều tính năng nhưng không có một tính năng nào cho phép chúng ta tính giới hạn của dãy số, muốn tính được giới hạn của dãy số thì phải sử dụng thủ thuật
Chúng ta sẽ tính giá trị của dãy số tại một số rất lớn sau đó quan sát màn hình máy tính rồi suy ra kết quả
Dưới đây là cách tính / bấm giới hạn lim của dãy số bằng máy tính cầm tay CASIO fx 880 BTG
1 Các bước thực hiện
Bước 1 nhập dãy số vào máy tính
Vì máy tính không có biến nhớ $n$ nên chúng ta sẽ nhập biến nhớ $x$
Bước 2 tiến hành CALC
Nhấn phím TOOLS => chọn CALC => nhập $10^9$ => nhấn phím EXE => nhấn phím EXE
Bước 3 quan sát giá trị hiển thị màn hình máy tính
Tùy thuộc vào giá trị đang hiển thị trên màn hình máy tính mà chúng ta sẽ suy ra kết quả
| Trường hợp | Nếu giá trị đang hiển thị trên màn hình máy tính có dạng … | … thì kết quả là … |
| 1 | $-a \times 10^n$ với $a \in R^+$ và $n \in N^*$ | $-\infty$ |
| 2 | $a \times 10^{-n}$ với $a \in R$ và $n \in N^*$ | $0$ |
| 3 | $a \times 10^n$ với $a \in R^+$ và $n \in N^*$ | $+\infty$ |
| 4 | $a$ với $a \in R^*$ | $a$ |
Chẳng hạn mình cần tính giới hạn của dãy số $\left({2+\frac{\left({-1}\right)^n}{n+2}}\right)$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1 nhập dãy số vào máy tính
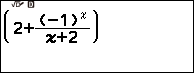
Bước 2 nhấn phím TOOLS => chọn CALC => nhấn phím OK

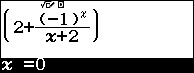
Bước 3 nhập $10^9$ => nhấn phím EXE => nhấn phím EXE
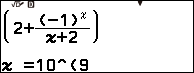
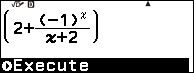
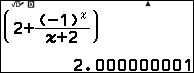
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 4 nên giới hạn của dãy số đã cho là $2$
Vậy $\lim\left({2+\frac{\left({-1}\right)^n}{n+2}}\right)=2$
2 Một số chú ý
- Cài đặt đơn vị góc là rađian nếu dãy số có chứa các hàm số lượng giác $\sin, \cos, \tan$
- CALC $10^6$ nếu dãy số có chứa các hàm số lượng giác $\sin, \cos, \tan$
- CALC $10^2$ nếu dãy số có chứ hàm số mũ
3 Ví dụ minh họa
Ví dụ 1 tính giới hạn của dãy số $\frac{\sin\left({3n}\right)}{4n}-1$
Dãy số đã cho có chứa hàm số lượng giác $\sin$ nên chúng ta cần cài đặt đơn vị góc là rađian và CALC $10^6$
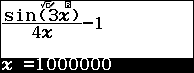
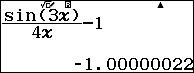
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 4 nên giới hạn của dãy số đã cho là $-1$
Vậy $\lim{\frac{\sin\left({3n}\right)}{4n}-1}=-1$
Ví dụ 2 tính giới hạn của dãy số $\frac{-2n^2+n+2}{3n^4+5}$
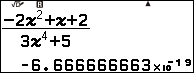
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 2 nên giới hạn của dãy số đã cho là $0$
Vậy $\lim\frac{-2n^2+n+2}{3n^4+5}=0$
Ví dụ 3 tính giới hạn của dãy số $\frac{4^n}{2\times3^n+4^n}$
Dãy số có chứa hàm số mũ nên chúng ta CALC $10^2$
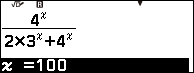
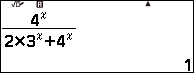
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 4 nên giới hạn của dãy số đã cho là $1$
Vậy $\lim \frac{4^n}{2\times3^n+4^n}=1$
Ví dụ 4 tính giới hạn của dãy số $-2n^3+3n+5$
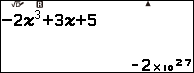
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 1 nên giới hạn của dãy số đã cho là $-\infty$
Vậy $\lim(-2n^3+3n+5)=-\infty$
Ví dụ 5 tính giới hạn của dãy số $\sqrt{3n^4+5n^3-7n}$
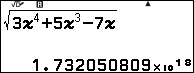
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 3 nên giới hạn của dãy số đã cho là $+\infty$
Vậy $\lim\sqrt{3n^4+5n^3-7n}=+\infty$
Ví dụ 6 tính giới hạn của dãy số $\frac{\sqrt[3]{n^6-7n^3-5n+8}}{n+12}$
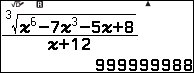

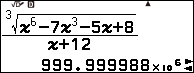
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 3 nên giới hạn của dãy số đã cho là $+\infty$
Vậy $\lim\frac{\sqrt[3]{n^6-7n^3-5n+8}}{n+12}=+\infty$
4 Bài tập thực hành
Bài tập 1 tính giới hạn của dãy số $\frac{n-1}{n}$

Vì giá trị trên màn hình máy tính rơi vào Trường hợp 4 nên giới hạn của dãy số đã cho là $1$
Vậy $\lim\frac{n-1}{n}=1$
Bài tập 2 tính giới hạn của dãy số $\frac{n+2}{n+1}$
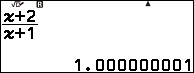
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 4 nên giới hạn của dãy số đã cho là $1$
Vậy $\lim\frac{n+2}{n+1}=1$
Bài tập 3 tính giới hạn của dãy số $\frac{n^2-3n+5}{2n^2-1}$
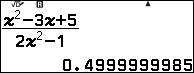
Vì giá trị trên màn hình máy tính rơi vào Trường hợp 4 nên giới hạn của dãy số đã cho là $\frac{1}{2}$
Vậy $\lim\frac{n^2-3n+5}{2n^2-1}=\frac{1}{2}$
https://youtube.com/shorts/mS5A1LyJFc4
5 Lời kết
Thủ thuật tính / bấm giới hạn lim của một dãy số bất kì bằng máy tính cầm tay CASIO fx 880 BTG không phải do mình sáng tạo ra
Mình chỉ là người cải tiến và thực hiện minh họa trên fx 880 BTG mà thôi
Thủ thuật này tuy rất hữu ích nhưng các bạn nên thực hành lại toàn bộ các ví dụ minh họa và bài tập để nhớ được các bước thực hiện và phiên dịch được từ giá trị hiển thị trên màn hình máy tính sang kết quả một cách nhanh chóng và chính xác
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo