Xin chào tất cả các bạn !
Phương trình nghiệm nguyên là một trong những lớp phương trình quan trọng trong Đại số.
Việc giải phương trình nghiệm nguyên không phải đơn giản vì không có phương pháp chung cho tất cả.
Tùy thuộc vào từng lớp phương trình nghiệm nguyên mà chúng ta sẽ có cách giải phù hợp.
Hôm nay, mình sẽ hướng dẫn các bạn giải nhanh phương trình nghiệm nguyên Pell $x^2-dy^2=1$ dưới sự hỗ trợ của máy tính cầm tay CASIO fx 880 BTG

https://www.youtube.com/watch?v=w-iMTeo_lAg
#1. Sơ lược về ý tưởng
Như các bạn đã biết để giải được phương trình Pell $x^2-dy^2=1$ chúng ta chỉ cần tìm ra nghiệm nguyên dương nhỏ nhất rồi áp dụng công thức nghiệm tổng quát là xong
Thông thường để tìm ra nghiệm nguyên dương nhỏ nhất chúng ta sẽ thực hiện hai bước:
Bước 1. Biểu diễn $\sqrt{d}$ sang liên phân số.
Bước 2. Tính các giản phân và tính giá trị biểu thức $P_i^2-dQ_i^2$
Về lí thuyết chúng ta luôn có thể thực hiện được Bước 1 và Bước 2, chỉ là chính xác hay chưa chính xác, nhanh hay chậm mà thôi.
Để tìm ra nghiệm nguyên dương nhỏ nhất bằng máy tính cầm tay …
- CASIO fx 580 VN X chúng ta có thể sử dụng tính năng biến nhớ, phần nguyên của giá trị và đa biểu thức
- CASIO fx 880 BTG chúng ta có thể sử dụng ứng dụng bảng tính Spreadsheet
Vì CASIO fx 880 BTG không thể ban hành vòng lập nên thủ thuật được trình bày bên dưới là một trong những thủ thuật tối ưu nhất
#2. Các bước giải phương trình nghiệm nguyên Pell
Chẳng hạn mình cần tìm nghiệm nguyên dương của phương trình Pell $x^2-dy^2=1$ thì thực hiện tuần tự theo các bước bên dưới.
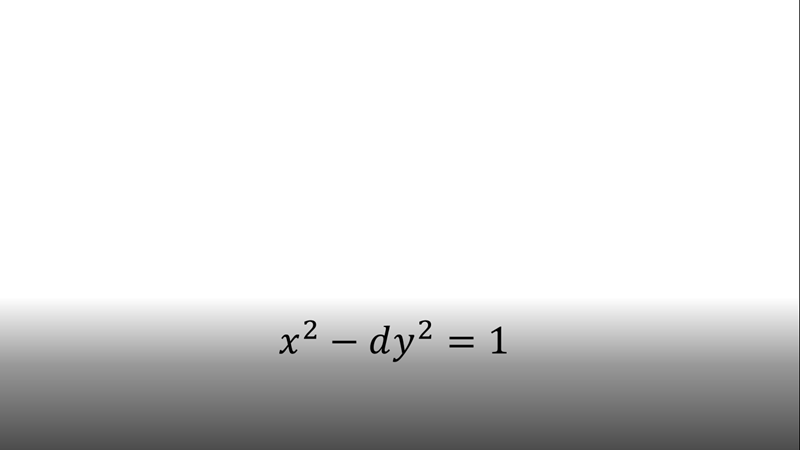
Bước 1. Mở bảng tính Spreadsheet
Bước 2. Biểu diễn $\sqrt{d}$ sang liên phân số
Bước 3. Tính các giản phân và tính giá trị biểu thức $P_i^2-dQ_i^2$
Giả sử $\sqrt{d}=[q_0; (q_1, q_2, q_3, …)]$
Bước 3.1. Lần lượt nhập $q_0, q_1, q_2, q_3, …$ vào các ô A1, A2, A3, …, A45
Bước 3.2. Nhập =A1 vào ô B1 và nhập =1 vào ô C1
Bước 3.3. Nhập $=A1 \times A2+1$ vào ô B2 và nhập =A2 vào ô C2
Bước 3.4. Ở ô B3 sử dụng Fill Formula với Form $A3 \times B2+B1$ và Range B3:B45
Bước 3.5. Ở ô C3 sử dụng Fill Formula với Form $A3 \times C2+C1$ và Range C3:C45
Bước 3.6. Ở ô D1 sử dụng Fill Formula với Form $B1^2-d \times C1^2$và Range D1:D45
Quan sát bảng tính, tìm đến ô $D_k$ sao cho $D_k=1$, lúc bấy giờ nghiệm nguyên dương nhỏ nhất là $(B_k, C_k)$
Vậy tập nghiệm nguyên dương của phương trình đã cho là $\left\{\begin{array}{l}x_n=\frac{(B_k+C_k\sqrt{d})^n+(B_k-C_k\sqrt{d})^n}{2}\\y_n=\frac{(B_k+C_k\sqrt{d})^n-(B_k-C_k\sqrt{d})^n}{2\sqrt{d}}\end{array}\right.$ với $n=1, 2, 3, …$
- A45, B45, C45 và D45 chỉ mang tính tương đối, khi thực hành tùy thuộc vào số lượng thương mà chúng ta sẽ xác định chính xác
- Trong trường hợp liên phân số có nhiều hơn 45 thương thì cần thực thêm một số thao tác phù hợp
#3. Thực hành giải phương trình
Chẳng hạn mình cần giải phương trình $x^2-14y^2=1$ thì thực hiện tuần tự theo các bước bên dưới
Bước 1. Mở bảng tính Spreadsheet
Nhấn phím HOME => chọn Spreadsheet => nhấn phím OK

Bước 2. Biểu diễn $\sqrt{14}$ sang liên phân số
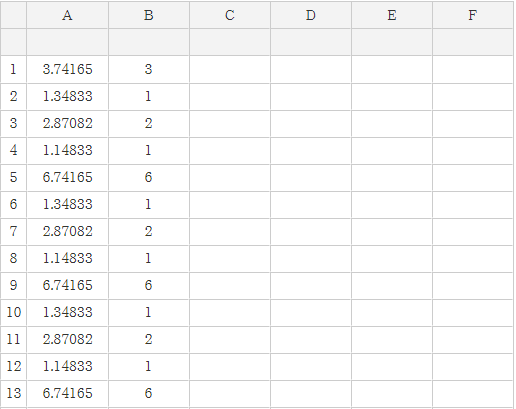
Suy ra $\sqrt{14}=[3; (1, 2, 1, 6)]$
Bước 3. tính các giản phân và tính giá trị biểu thức $P_i^2-14Q_i^2$
Bước 3.0. Nhấn phím ON để xóa toàn bộ dữ liệu trên bảng tính Spreadsheet

Bước 3.1. Lần lượt nhập 3, 1, 2, 1, 6 vào các ô A1, A2, A3, A4, A5
Nhập 3 => nhấn phím EXE => nhập 1 => nhấn phím EXE => nhập 2 => nhấn phím EXE => nhập 1 => nhấn phím EXE => nhập 6 => nhấn phím EXE
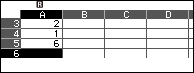
Bước 3.2. Nhập =A1 vào ô B1 và nhập =1 vào ô C1
Chọn ô B1 => nhập =A1 => nhấn phím EXE
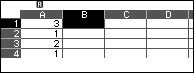
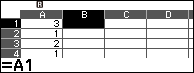
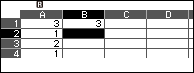
Chọn ô C1 => nhập =1 => nhấn phím EXE
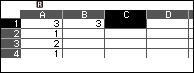
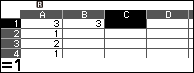
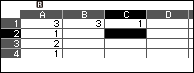
Bước 3.3. Nhập $=A1 \times A2+1$ vào ô B2 và nhập =A2 vào ô C2
Chọn ô B2 => nhập $=A1 \times A2+1$ => nhấn phím EXE
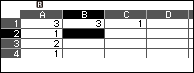
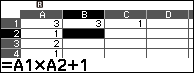
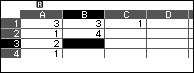
Chọn ô C2 => nhập =A2 => nhấn phím EXE
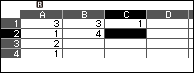
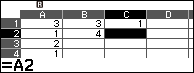
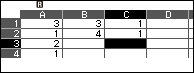
Bước 3.4. ở ô B3 sử dụng Fill Formula với Form $A3 \times B2+B1$ và Range B3:B5
Chọn ô B3
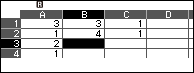
Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK => nhập $A3 \times B2+B1$ => nhấn phím EXE => nhập B3:B5 => nhấn phím EXE => nhấn phím EXE


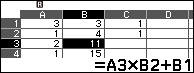
Bước 3.5. Ở ô C3 sử dụng Fill Formula với Form $A3 \times C2+C1$ và Range C3:C5
Chọn ô C3
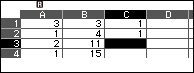
Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK => nhập $A3 \times C2+C1$ => nhấn phím EXE => nhập C3:C5 => nhấn phím EXE => nhấn phím EXE


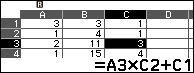
Bước 3.6. Ở ô D1 sử dụng Fill Formula với Form $B1^2-14 \times C1^2$ và Range D1:D5
Chọn ô D1
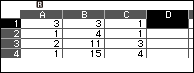
Nhấn phím TOOLS => chọn Fill Formula => nhấn phím OK => nhập $B1^2-14 \times C1^2$ => nhấn phím EXE => nhập D1:D5=> nhấn phím EXE => nhấn phím EXE


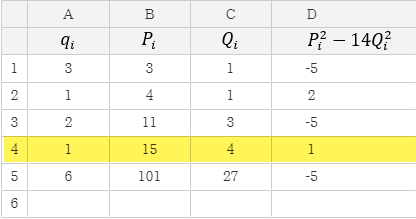
Quan sát bảng tính, chúng ta dễ dàng nhận thấy $D_4=1$ suy ra nghiệm nguyên dương nhỏ nhất là $(B_4=15, C_4=4)$
Vậy tập nghiệm nguyên dương của phương trình đã cho là $\left\{\begin{array}{l}x_n=\frac{(15+4\sqrt{14})^n+(15-4\sqrt{14})^n}{2}\\y_n=\frac{(15+4\sqrt{14})^n-(15-4\sqrt{14})^n}{2\sqrt{14}}\end{array}\right.$ với $n=1, 2, 3, …$
#4. Lời kết
Đáng tiếc là ứng dụng Spreadsheet của máy tính cầm tay CASIO fx 880 BTG chỉ có 5 cột, nếu có 8 cột chúng ta có thể giải phương trình nghiệm nguyên Pell $x^2-dy^2=1$ một cách nhanh chóng hơn nhiều
Cụ thể chúng ta sẽ thực hiện 3 công việc là biểu diễn $\sqrt{d}$ sang liên phân số, tính các giả phân và giá trị biểu thức $P_i^2-dQ_i^2$ chỉ với một lần duy nhất
Ngoài ra, các bạn có thể sử dụng ứng dụng bảng giá trị Table có gắng tìm trực tiếp nghiệm nguyên dương nhỏ nhất, tuy nhiên trong nhiều trường hợp khá khó tìm vì số lần thử quá nhiều
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo !