Xin chào tất cả các bạn, hôm nay mình sẽ hướng dẫn các bạn cách tính chỉnh hợp chập k của n phần tử bằng máy tính cầm tay CASIO fx 880 BTG
Trong bài viết này mình sẽ hướng dẫn cho các bạn tất cả ba cách, một cách sử dụng máy tính và hai cách sử dụng công thức Toán học
Sách giáo khoa thường kí hiệu chỉnh hợp chập $k$ của $n$ phần tử là $A_n^k$ còn fx 880 BTG là $nPk$
1 Nhắc lại một số kiến thức về chỉnh hợp
Cho tập hợp $A$ gồm $n$ phần tử $(n \geq 1)$
Kết quả của việc lấy $k$ phần tử khác nhau từ $n$ phần tử của tập hợp $A$ và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập $k$ của $n$ phần tử đã cho
Số các chỉnh hợp chập $k$ của $n$ phần tử $(1 \leq k \leq n)$ được kí hiệu là $A_n^k$ và được tính theo công thức $n(n-1)(n-2)(n-3) \cdots (n-k+1)=\frac{n!}{(n-k)!}$
2 Các cách tính số các chỉnh hợp chập k của n phần tử
Giả sử chúng ta cần tính số các chỉnh hợp chập $7$ của $11$
2.1 Cách 1 tính bằng máy tính cầm tay CASIO fx 880 BTG
Bước 1 nhập $n$ phần tử vào máy tính
Ở đây $n=11$ nên mình sẽ nhấn lần lượt các phím 
để nhập $11$ vào máy tính
Bước 2 nhấn phím CATALOG => chọn Probability => nhấn phím OK => chọn Permutation (P) => nhấn phím OK
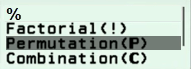
Bước 3 nhập $k$ vào máy tính
Ở đây $k=7$ nên mình sẽ nhấn phím 
để nhập $7$ vào máy tính
Bước 4 nhấn phím EXE để xem số các chỉnh hợp chập $k$ của $n$ phần tử
Vậy số các chỉnh hợp chập $7$ của $11$ là $1~663~200$
2.2 Cách 2 tính trực tiếp bằng công thức gốc
$A_{11}^7$
$=11(11-1)(11-2)(11-3)(11-4)(11-5)(11-6)$
$=11.10.9.8.7.6.5=1~663~200$
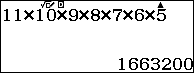
Vậy số các chỉnh hợp chập $7$ của $11$ là $1~663~200$
2.3 Cách 3 tính gián tiếp thông qua hoán vị / giai thừa
$A_{11}^7=\frac{11!}{(11-7)!}=1~663~200$
Vậy số các chỉnh hợp chập $7$ của $11$ là $1~663~200$
Xem thêm Cách tính hoán vị / giai thừa bằng CASIO fx 880 BTG
https://youtu.be/y2bVJAcMQGw
3 Lời kết
Tính năng tính số các chỉnh hợp chập $k$ của $n$ phần tử Permutation (P) trên máy tính cầm tay CASIO fx 880 BTG chính là tính năng / phím nPr trên fx 580 VN X
Nếu bạn nào đang sử dụng máy tính cầm tay CASIO fx 580 VN X thì vẫn tính được số các chỉnh hợp chập $k$ của $n$ phần tử một cách chính xác và nhanh chóng các bạn nhá (thậm chí thao tác còn nhanh hơn)
Xin chào tạm biệt và hẹn gặp lại các bạn trong những bài viết tiếp theo
